Point de Schiffler

En géométrie, le point de Schiffler d'un triangle est un centre de triangle, un point défini à partir du triangle qui est équivariant sous les transformations euclidiennes du triangle. Ce point a été défini et étudié pour la première fois par Schiffler et al. (1985). Il porte le nombre de Kimberling X21.

  • Triangle ABC
  • Les bissectrices, qui se croisent en I
  • Médianes des triangles intérieurs IAB, IBC, ICA
  • Médiatrices des segments de bissectrices [IA], [IB], [IC]
  • Droites d'Euler des triangles intérieurs, qui secroisent au point de Schiffler Sp

    • Définition

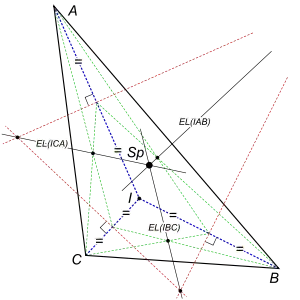
    Le point de Schiffer d'un triangle ABC de centre inscrit I est le point de concurrence des droites d'Euler des quatre triangles BCI, CAI, ABI et ABC. Le théorème de Schiffler stipule que ces quatre lignes se rejoignent toutes en un seul point.

    Coordonnées

    Les coordonnées trilinéaires du point de Schiffler sont

    ou encore,

    où a, b et c désignent les longueurs des côtés du triangle ABC, et A, B, C désignent les mesures d'angle aux sommets.

    Références
    • icône décorative Portail de la géométrie
    Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons – Attribution – Partage à l’identique. Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.