Trigyro-rhombicosidodécaèdre
En géométrie, le trigyro-rhombicosidodécaèdre est un des 92 solides de Johnson (J 75). Il contient 20 triangles, 30 carrés et 12 pentagones.
| Trigyro-rhombicosidodécaèdre | |
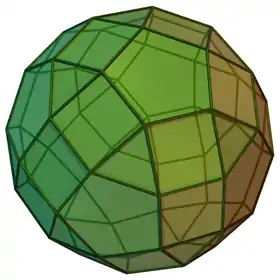
| |
| Type | Johnson J74 - J75 - J76 |
|---|---|
| Sommets | 60 |
| Arêtes | 120 |
| Faces | (nombre : 62) 2+2x3+2x6 = 20 t 4x3+3x6 = 30 c 4x3 = 12 p |
| Configuration faciale | triangles, carrés et pentagones |
| Groupe symétrique | Ih |
| Dual | - |
| Propriétés | convexe |
Il fait partie également des polyèdres canoniques.
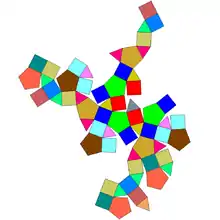
Développement du trigyro-rhombicosidodécaèdre
Comme son nom l'indique, ce polyèdre peut être obtenu à partir du rhombicosidodécaèdre en pivotant de 36 degrés trois des coupoles pentagonales.
Trois autres solides de Johnson sont également obtenus par rotation d'une ou plusieurs coupoles pentagonales: le gyro-rhombicosidodécaèdre (J72) avec une seule coupole pivotée, le parabigyro-rhombicosidodécaèdre (J73) avec deux coupoles opposées et le métabigyro-rhombicosidodécaèdre (J74) avec deux coupoles non opposées.
Liens externes
- Portail de la géométrie
Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons – Attribution – Partage à l’identique. Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.