Oloïde
L'oloïde, ou orthobicycle, est la surface obtenue comme enveloppe convexe de deux cercles orthogonaux passant chacun par le centre de l'autre. Paul Schatz en breveta la forme en 1929.
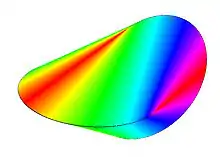
Définition
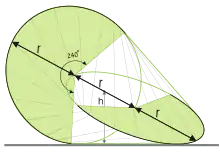
Comme le montre la figure de gauche, on considère deux cercles de même rayon r situés dans des plans perpendiculaires. Chaque cercle passe par le centre de l'autre. Ces deux cercles constituent la structure de l'oloïde.
On considère maintenant l'enveloppe convexe de ces deux cercles (traits verts). On remarque alors qu'une portion de chaque cercle se trouve à l'intérieur de l'enveloppe convexe. Cela montre que l'on aurait pu aussi définir l'oloïde comme l'enveloppe convexe d'arcs de cercle d'angle 240° chacun (dessinés sur la figure en noir).
L'oloïde est alors la surface (frontière) de cette enveloppe convexe.
Développement
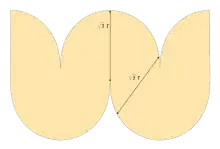
Cette surface est une partie de la surface développable s'appuyant sur deux cercles.
Applications industrielles
Plusieurs applications industrielles utilisent cette forme particulière (de se dérouler entièrement sur une surface plane sans frottement en oscillant de gauche à droite)[1] :
- Traitement des eaux usées et des milieux liquides.
- Agitateurs, brasseurs et aérateurs de surface.
- Centre de compostage.
Notes et références
Voir aussi
- Le sphéricône.
Liens externes
- [vidéo] L'objet qui te retourne le cerveau... (Oloïde) sur YouTube, chaine Dr Nozman.
- [vidéo] Incredible Rolling Objects which aren't Spheres! (Oloïde) sur YouTube, chaine Maker's Muse.
- Portail de la géométrie