Nombre octogonal

Pour avoir ${\displaystyle n}$ points sur chaque côté de l'octogone extérieur, on ajoute à l'étape ${\displaystyle n}$ : ${\displaystyle 8-1}$ points aux sommets et ${\displaystyle (8-2)(n-2)}$ points à l'intérieur des côtés, d'où ${\displaystyle O_{n}-O_{n-1}=7+6(n-2)=6(n-1)+1}$.

Donc ${\displaystyle O_{n}=\sum _{k=1}^{n}(6(k-1)+1)=\sum _{k=0}^{n-1}(6k+1)=3n(n-1)+n=n(3n-2)}$.

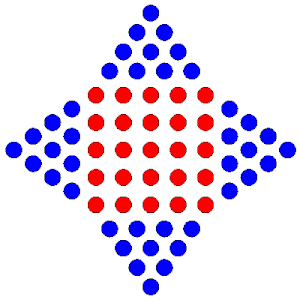
Nombre octogonal ${\displaystyle O_{5}=C_{5}+4T_{4}=25+4\times 10=65}$

De la formule générale ${\displaystyle P_{k,n}=P_{k-1,n}+T_{n-1}}$, découle par exemple que ${\displaystyle O_{n}}$ s'obtient en ajoutant le nombre carré ${\displaystyle C_{n}}$ au quadruple du ${\displaystyle (n-1)}$-ème nombre triangulaire : ${\displaystyle O_{n}=C_{n}+4T_{n-1}=n^{2}+2n(n-1)}$ .

• ${\displaystyle O_{n}=n+6T_{n-1}=n+3n(n-1)}$ est congru à ${\displaystyle n}$ modulo 6 et a donc même parité que lui.

• D'après le théorème des nombres polygonaux de Fermat, tout entier naturel est la somme d'au plus 8 nombres octogonaux.

• Nombre polygonal
• Nombre octogonal centré
• Nombre octaédrique

• Arithmétique et théorie des nombres