Loi logistique
En probabilité et en statistiques, la loi logistique est une loi de probabilité absolument continue à support infini utilisé en régression logistique et pour les réseaux de neurones à propagation avant. Son nom de loi logistique est issu du fait que sa fonction de répartition est une fonction logistique.
| Loi logistique | |
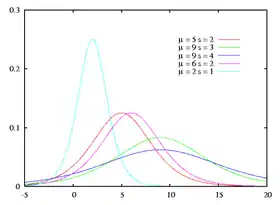 Densité de probabilité | |
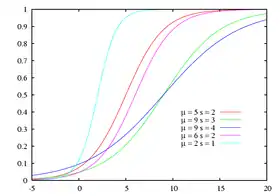 Fonction de répartition | |
| Paramètres | réel réel |
|---|---|
| Support | |
| Densité de probabilité | |
| Fonction de répartition | |
| Espérance | |
| Médiane | |
| Mode | |
| Variance | |
| Asymétrie | |
| Kurtosis normalisé | |
| Entropie | |
| Fonction génératrice des moments | pour , Fonction bêta |
| Fonction caractéristique | pour |
Définition et propriétés
La loi logistique a deux paramètres μ et s > 0 et sa densité est
Sa fonction de répartition est
Son espérance et sa variance sont données par les formules suivantes :
La loi logistique standard est la loi logistique de paramètres 0 et 1. Sa fonction de répartition est la sigmoïde :
Son espérance vaut alors 0 et sa variance π23.
Distributions associées
- Si alors .
- Si (loi uniforme continue) alors
- Si (loi de Gumbel) alors .
- Si (loi d'extremum généralisée) alors .
- Si alors .
- Si alors son exponentielle suit une loi log-logistique : , et (loi log-logistique à trois paramètres)
- Si (loi exponentielle) alors
- Si alors
Utilisations
La loi logistique est aussi utilisée pour le classement Elo.
Voir aussi
- Fonction logistique
- Régression logistique
- Logit
- Loi log-logistique
- Loi sécante hyperbolique
- Sigmoïde (mathématiques)
- Portail des probabilités et de la statistique
Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons – Attribution – Partage à l’identique. Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.