Logarithme itéré
En informatique, le logarithme itéré d'un nombre n, noté (lu "log star" ou "log étoile"), est le nombre de fois que le logarithme doit lui être appliqué avant que le résultat soit inférieur ou égal à 1. Cette fonction est utilisée pour décrire la complexité de certains algorithmes, notamment en algorithmique distribuée.
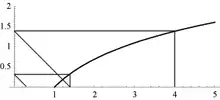
Définition
Le logarithme itéré de base b peut être défini par :
Sur les nombres réels positifs, le super-logarithme continu (l'inverse de la tétration) est essentiellement équivalente :
Le tableau suivant donne les valeurs du logarithme itéré (en base 2) :
| Si est dans l'intervalle... | Alors vaut : |
|---|---|
| 0 | |
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 |
Propriétés
Cette fonction croît extrêmement lentement. Une fonction usuelle en informatique théorique qui croît encore plus lentement est la réciproque de la fonction d'Ackermann. Ces deux fonctions sont d'ailleurs liées, puisque le logarithme itéré est l'un des niveaux de la hiérarchie de la réciproque d'Ackermann[1].
Utilisations
- Cette fonction est utilisée pour l'analyse d'algorithmes, par exemple pour exprimer la complexité de l'algorithme de triangulation de Delaunay et en algorithmique distribuée, par exemple dans la borne inférieure de Linial pour la coloration de graphe[2].
- Dasgupta et al., dans leur livre d'algorithmique, présente une analyse de complexité amortie de la structure de données union-find en utilisant le logarithme itéré[3].
- Le logarithme itéré intervient dans la complexité de l'algorithme de Fürer.
Notes et références
- Gabriel Nivasch, « Inverse Ackermann without pain », .
- Référence de l'article de Linial : (en) Nathan Linial, « Locality in Distributed Graph Algorithms », SIAM Journal on Computing, vol. 21, no 1, , p. 193-201.
- Sanjoy Dasgupta, Christos H. Papadimitriou et Umesh Vazirani, Algorithms, McGraw-Hill, Inc., (ISBN 0073523402 et 9780073523408, lire en ligne)
- Portail de l'analyse
- Portail de l'informatique théorique