Inégalité de Jordan

En mathématiques, l'inégalité de Jordan, du nom du mathématicien Camille Jordan, énonce que [1]

${\displaystyle {\frac {2}{\pi }}x\leqslant \sin x\leqslant x{\text{ pour }}x\in \left[0,{\frac {\pi }{2}}\right].}$

${\displaystyle {\frac {2}{\pi }}x\leqslant \sin(x)\leqslant x{\text{ pour }}x\in \left[0,{\frac {\pi }{2}}\right]}$

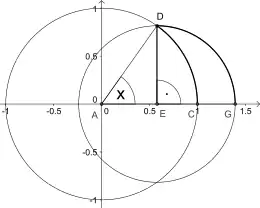
Cela peut être prouvé en utilisant la concavité de la fonction sinus dont la courbe est au-dessus de ses sécantes et en-dessous de ses tangentes[2], ou géométriquement comme ci-dessous[3].

Le cercle unité, et un cercle de rayon ${\displaystyle EG=\sin x}$ centré en E. ${\displaystyle {\begin{aligned}&DE\leqslant {\overset {\frown }{DC}}\leqslant {\overset {\frown }{DG}}\\\Leftrightarrow &\sin x\leqslant x\leqslant {\tfrac {\pi }{2}}\sin x\\\Leftrightarrow &{\tfrac {2}{\pi }}x\leqslant \sin x\leqslant x\end{aligned}}}$