Heptadécagone
Un heptadécagone est un polygone à 17 sommets, donc 17 côtés et 119 diagonales.
La somme des angles internes d'un heptadécagone non croisé vaut 15π radians, soit 2 700 degrés.
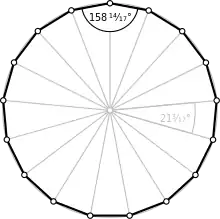
Dans l'heptadécagone régulier convexe, chaque angle interne vaut donc 15π/17 rad, soit environ 158,82°.
Heptadécagones réguliers
Un heptadécagone régulier est un heptadécagone dont les 17 côtés ont la même longueur et dont les angles internes ont même mesure. Il y en a huit : sept étoilés (les heptadécagrammes notés {17/k} pour k de 2 à 8) et un convexe (noté {17}). C'est de ce dernier qu'il s'agit lorsqu'on parle de « l'heptadécagone régulier ».
- Les sept heptadécagones réguliers étoilés
 {17/2}
{17/2} {17/3}
{17/3} {17/4}
{17/4} {17/5}
{17/5} {17/6}
{17/6} {17/7}
{17/7} {17/8}
{17/8}
Construction à la règle et au compas
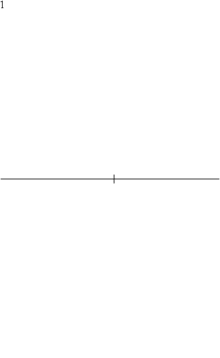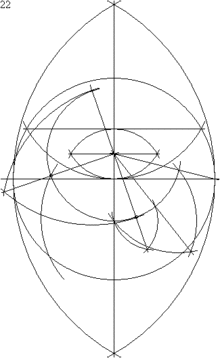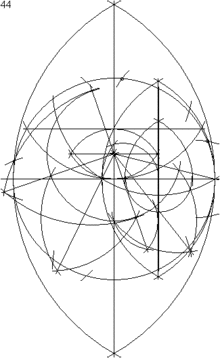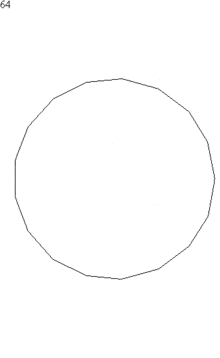
L'annonce de la construction à la règle et au compas de l'heptadécagone régulier a été faite par Carl Friedrich Gauss en 1796, et seulement dans un court article, Neue Entdeckungen, paru au numéro 66, du , de l'Intelligenzblatt der Allgemeinen Literatur-Zeitung de Iéna. Il fallut attendre cinq ans encore, avec la publication de ses Disquisitiones arithmeticae, pour découvrir la substance de cette construction (à l'article « Theorie von grösserem Umfange », en fin d'ouvrage).
Le sinus et le cosinus de l'angle sont respectivement égaux à :
- ;
- .
{{Démonstration |contenu=
Par définition, le problème de la construction de l'heptadécagone régulier revient à chercher les racines complexes du polynôme
On note α = 2π/17, puis on pose ω17 = exp(iα), et ωk = ωk
17, pour k entre 1 et 16, qui sont donc les racines recherchées.
On va construire des sommes de ces racines à partir de périodes qui forment les racines de polynômes du second degré[1]. On considère le tableau suivant, qui donne la valeur de, pour m entre 0 et 15, de 3m modulo 17 :
{{| class="wikitable centre" |- ! scope="row" | | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |- ! scope="row" | | 1 | 3 | 9 | 10 | 13 | 5 | 15 | 11 | 16 | 14 | 8 | 7 | 4 | 12 | 2 | 6 |- |}}
On utilise la congruence modulo 3 car 3 est une racine primitive de 17.
On pose donc les sommes :
Par les propriétés de symétrie, on peut observer que :
On peut remarquer, par les identités trigonométriques usuelles, que :
Ainsi, X1 et X2 sont les deux racines de X2 + X – 4 = 0, et une étude rapide de signe montre que X1 est la racine positive, et X1 > X2.
De même, on peut montrer que Y1 et Y2 sont les deux racines de Y2 + X1Y – 1 = 0, avec Y1 > Y2, et que Y3 et Y4 sont les deux racines de Y2 + X2Y – 1 = 0, avec Y3 > Y4.
Enfin, on peut vérifier que z1 = 2 cos α = ω1
17 + ω16
17 et z2 = 2 cos 4α = ω4
17 + ω13
17 sont les deux racines de Z2 – Y1Z + Y3 = 0, avec z1 > z2.
Il suffit dès lors de résoudre les équations du second degré et de ne retenir que les racines adéquates pour obtenir le résultat voulu. }}
On peut déduire des calculs précédents une construction de l'heptadécagone régulier à partir d'un cercle donné de centre O[2]:
- poser A et B sur le cercle tel que
- construire I tel que OI = 14OB
- construire E sur [OA] tel que
- construire F sur (OA) tel que
- construire le cercle de diamètre AF, il coupe [OB] en K
- le cercle de centre E et de rayon EK coupe (OA) en N3 et N5, avec N3 sur [OA]
- on construit P3 et P5, les projetés de N3 et N5 sur le cercle d'origine. Ces deux point sont deux sommets de l'heptadécagone, car et
Références
- (en) G. H. Hardy et E. M. Wright, An Introduction to the Theory of Numbers (lire en ligne)
- (en) H.W. Richmond, « A Construction for a Regular Polygon of Seventeen Sides », Quart. J. Pure Appl. Math., vol. 26, , p. 206-207 (lire en ligne)
Voir aussi
- (en) Eric W. Weisstein, « Heptadecagon », sur MathWorld
- (en) Eric W. Weisstein, « Trigonometry Angles — Pi/17 », sur MathWorld
- Portail de la géométrie