Hécatonicosachore
L'hécatonicosachore ou « 120-cellules » est un 4-polytope régulier convexe. C'est le dual de l'hexacosichore.
| Hécatonicosachore (120-cellules) | |
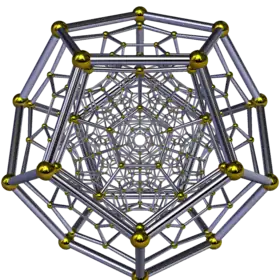 Diagramme de Schlegel (sommets et arêtes) | |
| Type | Polychore régulier |
|---|---|
| Cellules | 120 {5,3} |
| Faces | 720 {5} |
| Arêtes | 1200 |
| Sommets | 600 |
| Symbole de Schläfli | {5,3,3} |
| Polygone de Pétrie | Triacontagone |
| Groupe(s) de Coxeter | H4, [3,3,5] |
| Diagramme de Coxeter-Dynkin | |
| Dual | Hexacosichore (600-cellules) |
| Propriétés | Convexe, isogonal, isotoxal, isoédral |
Liens externes
- Comment dessiner un hécatonicosachore ? - sur le site « Images des maths » du CNRS.
- Portail de la géométrie
Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons – Attribution – Partage à l’identique. Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.